Différences entre les versions de « Mattias Desmet/2025.08.01 »
(Page créée avec « vignette ==Théorème de Bell - La lune existe-t-elle lorsque nous ne la regardons pas ?== Source : https://words.mattiasdesmet.org/p/bells-theorem-does-the-moon-exist {| class="wikitable" |- !VO!!VF |- |Dear friends, I have just spent a week at CERN, the world’s foremost research center for elementary particles. I was invited by a quantum physicist who had read my ''Psychology of Totalitarianism'' and who is providing thorough commenta... ») |
|||
| Ligne 9 : | Ligne 9 : | ||
!VO!!VF | !VO!!VF | ||
|- | |- | ||
|Dear friends, | |width=48%|Dear friends, | ||
I have just spent a week at CERN, the world’s foremost research center for elementary particles. I was invited by a quantum physicist who had read my ''Psychology of Totalitarianism'' and who is providing thorough commentary on the physics chapters of my next book as I write them. I spent a week among particle accelerators, discussing from morning till night the nature of matter and the collapse of the wave function. One thing I know for certain now: nobody in the world knows what matter is. I actually knew that beforehand, but I am glad to know that physicists know they don’t know either. | I have just spent a week at CERN, the world’s foremost research center for elementary particles. I was invited by a quantum physicist who had read my ''Psychology of Totalitarianism'' and who is providing thorough commentary on the physics chapters of my next book as I write them. I spent a week among particle accelerators, discussing from morning till night the nature of matter and the collapse of the wave function. One thing I know for certain now: nobody in the world knows what matter is. I actually knew that beforehand, but I am glad to know that physicists know they don’t know either. | ||
Version du 1 août 2025 à 19:46
Théorème de Bell - La lune existe-t-elle lorsque nous ne la regardons pas ?
Source : https://words.mattiasdesmet.org/p/bells-theorem-does-the-moon-exist
| VO | VF |
|---|---|
| Dear friends,
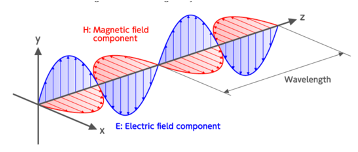
I have just spent a week at CERN, the world’s foremost research center for elementary particles. I was invited by a quantum physicist who had read my Psychology of Totalitarianism and who is providing thorough commentary on the physics chapters of my next book as I write them. I spent a week among particle accelerators, discussing from morning till night the nature of matter and the collapse of the wave function. One thing I know for certain now: nobody in the world knows what matter is. I actually knew that beforehand, but I am glad to know that physicists know they don’t know either. In the week before I went to CERN, I immersed myself in the famous Bell’s theorem. The Irish physicist John Bell is, together with Peter Higgs, perhaps the best-known CERN researcher ever. His theorem is sometimes described as the most intelligent piece of science ever conceived. It is this theorem that ultimately addressed the question Einstein once mockingly put to Niels Bohr: “Do you really think the moon doesn’t exist when you’re not looking at it?” On the internet you can find countless attempts to explain the theorem—some more successful than others. I have also made my own attempt to present the theorem in my own words. This explanation fits within a few chapters on physics in my new book. It is, at certain points, just a little too abstract to include in the book itself. That’s why I am posting it here. My presentation approaches the mathematics behind the theorem in as accessible a way as possible. I would say: don’t be intimidated by a few formulas and symbols—invest a little energy in the fascinating story of Bell’s theorem. .. At the beginning of the twentieth century, physics found itself in a tight spot. In 1802, Thomas Young had demonstrated through his famous double-slit experiment that light behaves like a wave. But in his miraculous year of 1905, Einstein had shown through his work on the photoelectric effect that light also behaves like a particle—at least under certain conditions. Both theories about light were logically coherent. Both were based on reproducible observations. But how can light be both a wave and a particle? The rift between these two perspectives was bridged by a new theory: the now-famous quantum physics. Yet in many ways, quantum theory is a torment for common sense. It makes predictions that appear absurd—so absurd, in fact, that even Einstein, who laid the foundation for quantum mechanics through his work on the photoelectric effect, remained deeply skeptical of it. Quantum theory claims, for example, that elementary particles — like all matter — do not exist in a definite state until they are observed. Before observation, they exist in a wave-like form that holds all possible properties at once — the so-called state of superposition. Einstein mocked this notion by asking Niels Bohr and his colleagues whether they truly believed the moon ceases to exist when we’re not looking at it. Quantum theory also proposes the existence of “entangled” particles — particles that are identical at the level of their wave functions and therefore must share corresponding properties. In other words: the properties of one particle are inextricably linked to those of another. This means that if you measure or manipulate one entangled particle, its twin — no matter how far away — instantly changes too. Since particles don’t assume definite properties until they’re observed, measuring one not only defines its own state, but also that of the other. So far, so good — or at least, so strange. In the famous 1935 Einstein-Podolsky-Rosen paper, the authors argued that something was seriously wrong with quantum theory. If the theory is correct, then the change in one entangled particle causes an instantaneous change in the other — “instantaneous” meaning “without the passage of any time.” If true, this would imply that the information travels faster than light. And if that were the case, Einstein argued, such communication would be not material, but immaterial. “I do not believe in spooky action at a distance,” he sneered. Einstein defended what’s known as “local realism.” Realism refers to the idea that particles exist independently of an observer. The entangled particles, once separated, may indeed respond to measurement or manipulation — but the way they respond depends on properties they already had, even if quantum theory doesn’t yet account for them. Local, meanwhile, means that particles cannot be influenced by events happening far away if there’s no material interaction between them. In other words: quantum theory’s claim that distant particles react to each other faster than light is absurd. Niels Bohr and the other quantum physicists stuck to their guns, though they admitted it would be extremely difficult — if not outright impossible — to prove their position through observation or experiment. Logically speaking, it seems impossible: how can you observe what properties a particle has before it’s been observed? But nearly thirty years after Einstein’s critical paper, Irish physicist John Bell would demonstrate that the impossible might just be possible. In 1964, he published a short paper introducing what would become known as Bell’s Theorem — showing that an experiment could be devised to determine who was right: Einstein or Bohr. ** We begin with an introductory explanation of the polarization—or vibration direction—of light. This property of light is important for understanding our explanation of Bell’s theorem. Light propagates (in wave form) as a transverse wave, meaning a wave whose vibration direction is perpendicular to the direction of propagation. Imagine a three-dimensional Cartesian coordinate system with orthogonal axes X, Y, and Z (see Figure 1). If the light wave moves in the direction of the Z-axis, then the wave oscillates perpendicular to Z—i.e., along a vector lying in the X-Y plane. The direction in which the wave vibrates is called the polarization of the light. Light can consist of waves that all share the same polarization or have different vibration directions. The left part of Figure 1 illustrates this. There you see a beam of light traveling in a horizontal direction, made up of light waves oscillating in various directions perpendicular to that horizontal arrow. Some types of light, such as sunlight, exhibit all polarizations—that is, they contain waves oscillating in every possible direction within the X-Y plane
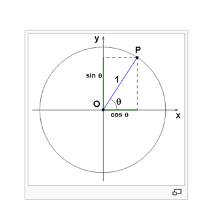
P(0°) = 100% Light waves that vibrate in a direction perpendicular to the slats will all be blocked. In this case, the angle between the polarization vector and the transmission axis is 90°, so the probability of transmission is 0%. In formula: P(90°) = 0% For light waves whose polarization vector forms an angle between 0° and 90° with the transmission axis, the probability of being blocked increases as the angle approaches 90°. You can calculate this probability using the sine squared of the angle X. A quick trigonometry refresher: the sine of an angle is simply the projection of the radius of a circle onto the vertical axis under that angle (see Figure 3).
P(X) = sin²(X) When light with multiple polarizations strikes a polarizing filter, the filter will block (absorb or reflect) some of the light waves and allow others to pass through. The probability that a light wave passes through depends, as shown in the formula, on how closely the light’s polarization direction aligns with the transmission direction of the filter. That concludes our short introduction to the physics of light. Now we move on to Bell’s theorem. ** As mentioned earlier, Bell had devised something that allowed one to experimentally test whether entangled particles do or do not possess all their properties prior to observation, and whether or not they can “spookily” communicate with each other at a speed faster than light. Imagine an experiment in which two entangled particles are emitted simultaneously and in opposite directions. In each direction, a scientist is waiting with three polarizing filters at their disposal:
The two particles travel at the same speed (the speed of light), and the filters are placed at precisely equal distances from the source, so that both particles reach their respective filters at exactly the same time. In the experiment, three series are carried out, each consisting of a large number of entangled particle pairs—let’s say a few hundred.
This setup results in the following filter combinations for each entangled pair:
You may wonder why we are only considering these specific combinations of filters in the experiment. That is a good question. As you’ll soon see, the other combinations are indeed unnecessary. At first glance, this experiment seems to make no progress at all in determining whether Einstein or Bohr was right. In fact, Einstein predicted exactly the same filter results as Bohr. According to both theories, the particles would either pass through certain filters or not, in the same way. The difference between Einstein’s and Bohr’s theories lies entirely in the explanation of the particles’ behavior—not in the behavior itself. Einstein believed that the particles already “knew” in advance whether they would pass through a given filter or not—simply because all their properties were already determined beforehand. Bohr, on the other hand, believed that—for reasons beyond our reach—the particles made that choice at the moment of measurement, and only then acquired the properties that would determine whether they would pass or not. In a flash of genius, Bell realized that Einstein’s and Bohr’s theories actually do make different predictions. The statistical probability that entangled light particles pass through the filter differs depending on whether the calculation is based on the assumption that Einstein’s theory (i.e., local realism) is correct, or whether it is based on the assumption that Bohr’s theory (i.e., quantum theory) is correct. We will now go ahead and perform the calculation of both probabilities. ** If Einstein is right, then the particles already possess the properties in advance that will determine whether or not they pass through the filter. We don’t know those properties—they are hidden variables—but they are definitely already there beforehand. That’s simply the reasoning that our common sense provides. Reality and matter exist, whether we are looking at them or not. Bell realized that in this case, you cannot precisely calculate the probability that the particles will or won’t pass through the filter (since you don’t know the relevant properties in advance), but you can determine a ratio or inequality in the probability distributions across the three conditions (i.e., the three series of particle pairs fired) of the experiment, based on simple logic. We use the following symbols in laying out that logic:
Here we go. If Einstein is right and the properties of the elementary particles are fixed in advance, then it is also fixed in advance whether a particle will or will not pass through filter A, B, or C. Based on the following simple (algebraic) logic, we can then say something about the probability that a particle has the potential to pass through combinations of filters A, B, and C: (1) P(AB̄) ≥ P(AB̄C̄) According to our notation, we read this as:“The probability that a particle passes through filter A and not through filter B is greater than or equal to the probability that it passes through filter A and not through filter B and not through filter C.” There’s no arguing with that—it is as logically sound as anything can be. In the same way, we arrive at the following expressions: (2) P(BC̄) ≥ P(ABC̄) (3) P(AC̄) = P(AB̄C̄) + P(ABC̄) From the combination of (1), (2), and (3), we can very simply derive: (4) P(AC̄) ≤ P(AB̄) + P(BC̄) In this way, Bell determined a specific inequality between the probabilities that a particle would or would not pass through certain combinations of filters. ** We can now determine exactly the same probabilities under the condition that it is not Einstein but rather Bohr (i.e., quantum mechanics) who is right. For this, he used a different kind of calculation. Quantum mechanics assumes that a particle only acquires its properties at the moment those properties are registered or measured. For example, the polarization direction of a particle can “come into being” as it passes through a filter and is thereby “measured.” That is precisely what we do in the experiment described here: we send particles through a filter and thereby determine their polarization. Since, according to Bohr, the particle has no polarization before passing through the filter, it always has a 50% chance of passing through any filter. It is precisely at this point that the difference between Einstein’s theory and Bohr’s theory becomes relevant. According to Einstein, each particle has an unknown but definite chance of passing a filter, depending on its pre-existing, hidden properties. According to Bohr, each particle has exactly a 50% chance (½) of passing through any filter. At the moment the particle passes through the first filter, its polarization direction becomes fixed/materialized, and from that point on, there is a definite probability that it can pass through another filter. Let us note here: in our experiment, the two particles pass through their respective filters at exactly the same time. Is that a problem? No. We can arbitrarily designate one of the two filters as the “first,” and the rest of the reasoning proceeds accordingly. So: the probability that the particle passes the first filter is always 50%. The probability that it passes the second filter depends on the difference in angle between the transmission axes of the two filters. As we showed earlier, we can calculate that probability by squaring the sine of that angle. Using this, we can calculate each of the probabilities that appear in the inequality we derived earlier under the assumption that Einstein was right. We first calculate the probability that a particle passes through filter A but not through filter C. The angle between the transmission axes of filters A and C is 45° (see earlier). The formula to calculate the probability that a particle passes A but not C is: (1) P(AC̄) = 50% * sin²(45°) = 50% * 0.500 = 25% If we apply the same formula to the two other relevant probabilities, we get: (2) P(AB̄) = 50% * sin²(22.5°) = 50% * 0.146 = 7.3% (3) P(BC̄) = 50% * sin²(22.5°) = 50% * 0.146 = 7.3% Now comes the key point. If we fill in these values in the probability inequality that we derived under the assumption that Einstein was right, we see that they are incompatible. Let’s do that. Under the condition that Einstein was right, we found the following inequality (see earlier): P(AC̄) < P(AB̄) + P(BC̄) If we now substitute the values we calculated under the assumption that Bohr was right, we get: 25% < 7.3% + 7.3% Which is clearly false. In other words: Bell’s theorem shows that—contrary to the initial impression—Einstein’s and Bohr’s theories do not predict the same outcomes, and that an experiment can, in fact, determine which one of the two was right. ** At that time, the equipment required to carry out the experiment was not yet sufficiently advanced. It wasn’t until 1982 that this became the case. Alain Aspect then tested Bell’s theorem, and the outcome left no room for doubt: Einstein was wrong, Bohr was right. The consequences for our view of reality are enormous. The test of Bell’s theorem showed that elementary particles are wave patterns in a state of superposition before being observed, and that they communicate with each other ‘timelessly’ over any distance. Since these elementary particles are the building blocks of our entire reality, this implies that our entire reality is in superposition as long as it is not observed. What is true for each tiny brick of a house is, in a sense, also true for the house itself. Einstein once sneered at Bohr: “Do you really believe that the moon ceases to exist if you’re not looking at it?” We can now answer him: Indeed. Or at least: it does not exist in the way it exists when we are looking at it. Man is a co-creator of the reality in which he lives; he does not passively undergo it. But what exactly causes the wave in superposition to become a particle? Is it the act of measuring, or the act of observing? The most conservative stance is to claim that it is the material measuring apparatus that changes what is being observed. In that case, one still clings—if only with one hand—tightly to the branches of the materialist trees. Most academic physicists probably opt for this position. But then I wonder: Einstein wasn’t referring to the material act of measuring when he mentioned the moon; he was talking about looking at the moon. He clearly interpreted quantum theory as a theory that believes it is the act of looking that is decisive (even without measuring equipment). Likewise, I wonder: we do not see the world around us as a wave in superposition, but as a collection of particles with more or less fixed properties. Does this not imply that the act of looking itself caused the wave function to collapse, and that the particle became a fixed particle? To paraphrase Einstein: Do we really believe that the collapse of the wave function does not occur if there are no physicists measuring particles? Finally: in the many variations of the double-slit experiment, it turns out that a wave becomes a particle precisely at the moment the camera that registers it actually makes an unambiguous registration. For instance, if electrons are fired at the double slits and we register the exact position of the electron with a camera using light frequencies, then it is observed that exactly at the moment the light frequency becomes high enough to register the electron, the wave pattern collapses and the electron becomes a particle. These experimental findings also suggest, in my opinion, that what is decisive is not the material measuring apparatus itself—which remains the same, regardless of the light frequency—but rather the act of registering or observing itself. In other words: it is the ‘act of consciousness’ in observation that is decisive. Lastly, it is the case that the founders of quantum theory, based on their theory and their observations, declared the materialist worldview to be incorrect, and leaned toward a mystical or idealist worldview, in which consciousness is regarded as the cause of matter (and not the other way around, as materialism claims). And if we see how even someone as admirable as Niels Bohr vacillated somewhat on this theme—sometimes warm, sometimes cold—then perhaps we must ultimately conclude that even the greatest among us did not entirely overcome a certain fear of the (materialist) masses. Mattias |
Chers amis, je viens de passer une semaine au CERN,
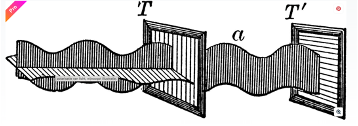
Je viens de passer une semaine au CERN, le plus grand centre mondial de recherche sur les particules élémentaires. J'ai été invité par un physicien quantique qui a lu ma Psychologie du totalitarisme et qui commente en profondeur les chapitres de physique de mon prochain livre au fur et à mesure que je les écris. J'ai passé une semaine au milieu des accélérateurs de particules, discutant du matin au soir de la nature de la matière et de l'effondrement de la fonction d'onde. Une chose est sûre : personne au monde ne sait ce qu'est la matière. En fait, je le savais déjà, mais je suis heureux de savoir que les physiciens savent qu'ils ne le savent pas non plus. La semaine précédant mon départ pour le CERN, je me suis plongé dans le célèbre théorème de Bell. Le physicien irlandais John Bell est, avec Peter Higgs, peut-être le chercheur le plus connu du CERN. Son théorème est parfois décrit comme l'œuvre scientifique la plus intelligente jamais conçue. C'est ce théorème qui a permis de répondre à la question qu'Einstein a posée à Niels Bohr en se moquant de lui : "Pensez-vous vraiment que la lune n'existe pas quand vous ne la regardez pas ? Sur Internet, on trouve d'innombrables tentatives d'explication du théorème, certaines plus réussies que d'autres. J'ai également tenté de présenter le théorème dans mes propres mots. Cette explication s'inscrit dans les quelques chapitres de physique de mon nouveau livre. À certains moments, elle est un peu trop abstraite pour être incluse dans le livre lui-même. C'est pourquoi je la publie ici. Ma présentation aborde les mathématiques qui sous-tendent le théorème d'une manière aussi accessible que possible. Je dirais : ne vous laissez pas intimider par quelques formules et symboles - investissez un peu d'énergie dans l'histoire fascinante du théorème de Bell. .. Au début du XXe siècle, la physique se trouvait dans une situation délicate. En 1802, Thomas Young avait démontré par sa célèbre expérience de la double fente que la lumière se comporte comme une onde. Mais en 1905, année miraculeuse, Einstein avait démontré, grâce à ses travaux sur l'effet photoélectrique, que la lumière se comportait également comme une particule, du moins dans certaines conditions. Les deux théories sur la lumière étaient logiquement cohérentes. Elles étaient toutes deux fondées sur des observations reproductibles. Mais comment la lumière peut-elle être à la fois une onde et une particule ? Le fossé entre ces deux perspectives a été comblé par une nouvelle théorie : la désormais célèbre physique quantique. Pourtant, à bien des égards, la théorie quantique est un supplice pour le sens commun. Elle fait des prédictions qui semblent absurdes, à tel point que même Einstein, qui a jeté les bases de la mécanique quantique grâce à ses travaux sur l'effet photoélectrique, est resté profondément sceptique à son égard. La théorie quantique affirme, par exemple, que les particules élémentaires - comme toute matière - n'existent pas dans un état défini avant d'être observées. Avant l'observation, elles existent sous une forme ondulatoire qui contient toutes les propriétés possibles à la fois - ce que l'on appelle l'état de superposition. Einstein s'est moqué de cette notion en demandant à Niels Bohr et à ses collègues s'ils croyaient vraiment que la lune cessait d'exister lorsque nous ne la regardions pas. La théorie quantique propose également l'existence de particules "intriquées", c'est-à-dire de particules qui sont identiques au niveau de leurs fonctions d'onde et qui doivent donc partager des propriétés correspondantes. En d'autres termes, les propriétés d'une particule sont inextricablement liées à celles d'une autre. Cela signifie que si vous mesurez ou manipulez une particule intriquée, sa jumelle, aussi éloignée soit-elle, change instantanément. Étant donné que les particules n'acquièrent des propriétés définitives que lorsqu'elles sont observées, le fait de mesurer l'une d'entre elles définit non seulement son propre état, mais aussi celui de l'autre. Jusqu'ici, tout va bien - ou du moins, tout est étrange. Dans le célèbre article d'Einstein-Podolsky-Rosen de 1935, les auteurs affirment que quelque chose ne va pas dans la théorie quantique. Si la théorie est correcte, le changement d'une particule intriquée entraîne un changement instantané de l'autre - "instantané" signifiant "sans écoulement de temps". Si c'est le cas, cela signifie que l'information voyage plus vite que la lumière. Si tel était le cas, cette communication ne serait pas matérielle, mais immatérielle, selon Einstein. "Je ne crois pas à l'effet de surprise à distance", ironise-t-il. Einstein a défendu ce que l'on appelle le "réalisme local". Le réalisme fait référence à l'idée que les particules existent indépendamment d'un observateur. Les particules intriquées, une fois séparées, peuvent en effet réagir à une mesure ou à une manipulation, mais la manière dont elles réagissent dépend des propriétés qu'elles possèdent déjà, même si la théorie quantique ne les prend pas encore en compte. Le terme "local", quant à lui, signifie que les particules ne peuvent pas être influencées par des événements qui se produisent à distance s'il n'y a pas d'interaction matérielle entre elles. En d'autres termes, l'affirmation de la théorie quantique selon laquelle des particules éloignées réagissent les unes aux autres plus vite que la lumière est absurde. Niels Bohr et les autres physiciens quantiques sont restés sur leurs positions, tout en admettant qu'il serait extrêmement difficile, voire impossible, de prouver leur position par l'observation ou l'expérience. Logiquement, cela semble impossible : comment observer les propriétés d'une particule avant qu'elle n'ait été observée ? Mais près de trente ans après l'article critique d'Einstein, le physicien irlandais John Bell allait démontrer que l'impossible pouvait être possible. En 1964, il a publié un court article présentant ce qui allait devenir le théorème de Bell, montrant qu'une expérience pouvait être conçue pour déterminer qui avait raison : Einstein ou Bohr. ** Nous commençons par une explication introductive de la polarisation - ou direction de vibration - de la lumière. Cette propriété de la lumière est importante pour comprendre notre explication du théorème de Bell. La lumière se propage (sous forme d'onde) comme une onde transversale, c'est-à-dire une onde dont la direction de vibration est perpendiculaire à la direction de propagation. Imaginons un système de coordonnées cartésiennes tridimensionnel avec des axes orthogonaux X, Y et Z (voir figure 1). Si l'onde lumineuse se déplace dans la direction de l'axe Z, elle oscille perpendiculairement à Z, c'est-à-dire le long d'un vecteur situé dans le plan X-Y. La direction dans laquelle l'onde vibre est perpendiculaire à la direction de propagation. La direction dans laquelle l'onde vibre est appelée polarisation de la lumière. La lumière peut être constituée d'ondes qui partagent toutes la même polarisation ou qui ont des directions de vibration différentes. La partie gauche de la figure 1 illustre ce phénomène. On y voit un faisceau de lumière se déplaçant dans une direction horizontale, composé d'ondes lumineuses oscillant dans différentes directions perpendiculaires à la flèche horizontale. Certains types de lumière, comme la lumière du soleil, présentent toutes les polarisations, c'est-à-dire qu'ils contiennent des ondes oscillant dans toutes les directions possibles à l'intérieur du plan X-YP(0°) = 100% Les ondes lumineuses qui vibrent dans une direction perpendiculaire aux lamelles seront toutes bloquées. Dans ce cas, l'angle entre le vecteur de polarisation et l'axe de transmission est de 90°, la probabilité de transmission est donc de 0 %. La formule est la suivante P(90°) = 0% Pour les ondes lumineuses dont le vecteur de polarisation forme un angle compris entre 0° et 90° avec l'axe de transmission, la probabilité d'être bloqué augmente lorsque l'angle se rapproche de 90°. Vous pouvez calculer cette probabilité en utilisant le carré du sinus de l'angle X. Petit rappel de trigonométrie : le sinus d'un angle est simplement la projection du rayon d'un cercle sur l'axe vertical sous cet angle (voir figure 3).P(X) = sin²(X) Lorsque de la lumière à polarisations multiples frappe un filtre polarisant, celui-ci bloque (absorbe ou réfléchit) certaines ondes lumineuses et en laisse passer d'autres. La probabilité qu'une onde lumineuse passe dépend, comme le montre la formule, du degré d'alignement de la direction de polarisation de la lumière avec la direction de transmission du filtre. Voilà qui conclut notre brève introduction à la physique de la lumière. Passons maintenant au théorème de Bell. ** Comme nous l'avons déjà mentionné, Bell a mis au point un dispositif qui permet de tester expérimentalement si des particules intriquées possèdent ou non toutes leurs propriétés avant d'être observées, et si elles peuvent ou non communiquer entre elles à une vitesse supérieure à celle de la lumière, ce qui est assez effrayant. Imaginez une expérience dans laquelle deux particules intriquées sont émises simultanément et dans des directions opposées. Dans chaque direction, un scientifique attend avec trois filtres polarisants à sa disposition :
Les deux particules se déplacent à la même vitesse (vitesse de la lumière) et les filtres sont placés à des distances exactement égales de la source, de sorte que les deux particules atteignent leurs filtres respectifs exactement au même moment. Dans l'expérience, trois séries sont réalisées, chacune consistant en un grand nombre de paires de particules intriquées - disons quelques centaines.
Cette configuration donne les combinaisons de filtres suivantes pour chaque paire intriquée :
Vous vous demandez peut-être pourquoi nous ne considérons que ces combinaisons spécifiques de filtres dans l'expérience. C'est une bonne question. Comme vous le verrez bientôt, les autres combinaisons sont en effet inutiles. À première vue, cette expérience ne permet pas du tout de déterminer si Einstein ou Bohr avait raison. En fait, Einstein a prédit exactement les mêmes résultats de filtrage que Bohr. Selon les deux théories, les particules passeraient ou non à travers certains filtres, de la même manière. La différence entre les théories d'Einstein et de Bohr réside entièrement dans l'explication du comportement des particules, et non dans le comportement lui-même. Einstein pensait que les particules "savaient" déjà à l'avance si elles allaient passer à travers un filtre donné ou non, simplement parce que toutes leurs propriétés étaient déjà déterminées à l'avance. Bohr, quant à lui, pensait que, pour des raisons qui nous échappent, les particules faisaient ce choix au moment de la mesure et n'acquéraient qu'ensuite les propriétés qui détermineraient si elles passeraient ou non. Dans un éclair de génie, Bell a réalisé que les théories d'Einstein et de Bohr faisaient en réalité des prédictions différentes. La probabilité statistique que des particules de lumière intriquées passent à travers le filtre diffère selon que le calcul est basé sur l'hypothèse que la théorie d'Einstein (c'est-à-dire le réalisme local) est correcte ou sur l'hypothèse que la théorie de Bohr (c'est-à-dire la théorie quantique) est correcte. Nous allons maintenant calculer les deux probabilités. ** Si Einstein a raison, alors les particules possèdent déjà à l'avance les propriétés qui détermineront si elles passent ou non à travers le filtre. Nous ne connaissons pas ces propriétés - ce sont des variables cachées - mais elles sont déjà présentes à l'avance. C'est simplement le raisonnement que nous fournit notre sens commun. La réalité et la matière existent, que nous les regardions ou non. Bell s'est rendu compte que dans ce cas, on ne peut pas calculer précisément la probabilité que les particules passent ou non à travers le filtre (puisqu'on ne connaît pas les propriétés pertinentes à l'avance), mais on peut déterminer un rapport ou une inégalité dans les distributions de probabilité entre les trois conditions (c'est-à-dire les trois séries de paires de particules tirées) de l'expérience, sur la base d'une logique simple. Nous utilisons les symboles suivants pour présenter cette logique :
Nous y voilà. Si Einstein a raison et que les propriétés des particules élémentaires sont fixées à l'avance, alors il est également fixé à l'avance si une particule passera ou non à travers les filtres A, B ou C. Sur la base de la logique (algébrique) simple suivante, nous pouvons alors dire quelque chose sur la probabilité qu'une particule ait le potentiel de passer à travers les combinaisons de filtres A, B et C : (1) P(AB̄) ≥ P(AB̄C̄) Selon notre notation, nous lisons ceci comme : "La probabilité qu'une particule passe par le filtre A et non par le filtre B est supérieure ou égale à la probabilité qu'elle passe par le filtre A et non par le filtre B et non par le filtre C." Il n'y a rien à redire à cela, c'est aussi logique qu'il soit possible de l'être. De la même manière, nous arrivons aux expressions suivantes : (2) P(BC̄) ≥ P(ABC̄) (3) P(AC̄) = P(AB̄C̄) + P(ABC̄) De la combinaison de (1), (2), et (3), nous pouvons très simplement dériver : (4) P(AC̄) ≤ P(AB̄) + P(BC̄) De cette manière, Bell a déterminé une inégalité spécifique entre les probabilités qu'une particule passe ou ne passe pas à travers certaines combinaisons de filtres. ** Nous pouvons maintenant déterminer exactement les mêmes probabilités à condition que ce ne soit pas Einstein mais Bohr (c'est-à-dire la mécanique quantique) qui ait raison. Pour cela, il a utilisé un autre type de calcul. La mécanique quantique part du principe qu'une particule n'acquiert ses propriétés qu'au moment où celles-ci sont enregistrées ou mesurées. Par exemple, la direction de polarisation d'une particule peut "naître" lorsqu'elle passe à travers un filtre et est ainsi "mesurée". C'est précisément ce que nous faisons dans l'expérience décrite ici : nous envoyons des particules à travers un filtre et déterminons ainsi leur polarisation. Comme, selon Bohr, la particule n'a pas de polarisation avant de passer à travers le filtre, elle a toujours une chance sur deux de passer à travers n'importe quel filtre. C'est précisément à ce stade que la différence entre la théorie d'Einstein et celle de Bohr devient pertinente. Selon Einstein, chaque particule a une chance inconnue mais définie de passer un filtre, en fonction de ses propriétés préexistantes et cachées. Selon Bohr, chaque particule a exactement 50 % de chances (½) de passer à travers n'importe quel filtre. Au moment où la particule traverse le premier filtre, sa direction de polarisation devient fixe/matérialisée, et à partir de ce moment, il y a une probabilité certaine qu'elle puisse traverser un autre filtre. Notons ici que dans notre expérience, les deux particules traversent leurs filtres respectifs exactement au même moment. Cela pose-t-il un problème ? Non. Nous pouvons désigner arbitrairement l'un des deux filtres comme étant le "premier", et le reste du raisonnement se déroule en conséquence. Ainsi, la probabilité que la particule passe le premier filtre est toujours de 50 %. La probabilité qu'elle passe le second filtre dépend de la différence d'angle entre les axes de transmission des deux filtres. Comme nous l'avons montré précédemment, nous pouvons calculer cette probabilité en élevant au carré le sinus de cet angle. Ainsi, nous pouvons calculer chacune des probabilités qui apparaissent dans l'inégalité que nous avons dérivée plus tôt en supposant qu'Einstein avait raison. Nous calculons d'abord la probabilité qu'une particule passe à travers le filtre A mais pas à travers le filtre C. L'angle entre les axes de transmission des filtres A et C est de 45° (voir plus haut). La formule pour calculer la probabilité qu'une particule passe par A mais pas par C est la suivante : (1) P(AC̄) = 50% * sin²(45°) = 50% * 0,500 = 25% Si nous appliquons la même formule aux deux autres probabilités pertinentes, nous obtenons : (2) P(AB̄) = 50% * sin²(22.5°) = 50% * 0.146 = 7.3%. (3) P(BC̄) = 50% * sin²(22,5°) = 50% * 0,146 = 7,3%. Voici maintenant le point clé. Si nous remplissons ces valeurs dans l'inégalité de probabilité que nous avons dérivée en supposant qu'Einstein avait raison, nous constatons qu'elles sont incompatibles. C'est ce que nous allons faire. Si Einstein avait raison, nous avons trouverions l'inégalité suivante (voir plus haut) : P(AC̄) < P(AB̄) + P(BC̄) Si nous remplaçons maintenant les valeurs que nous avons calculées en supposant que Bohr avait raison, nous obtenons : 25% < 7.3% + 7.3% Ce qui est clairement faux. En d'autres termes : Le théorème de Bell montre que, contrairement à l'impression initiale, les théories d'Einstein et de Bohr ne prédisent pas les mêmes résultats, et qu'une expérience peut, en fait, déterminer laquelle des deux avait raison. ** À l'époque, le matériel nécessaire pour réaliser l'expérience n'était pas encore suffisamment perfectionné. Il faudra attendre 1982 pour que ce soit le cas. Alain Aspect teste alors le théorème de Bell et le résultat ne laisse aucune place au doute : Einstein avait tort, Bohr avait raison. Les conséquences sur notre vision de la réalité sont énormes. Le test du théorème de Bell a montré que les particules élémentaires sont des modèles d'ondes dans un état de superposition avant d'être observées, et qu'elles communiquent entre elles "hors du temps" sur n'importe quelle distance. Comme ces particules élémentaires sont les éléments constitutifs de toute notre réalité, cela implique que toute notre réalité est en superposition tant qu'elle n'est pas observée. Ce qui est vrai pour chaque petite brique d'une maison l'est aussi, d'une certaine manière, pour la maison elle-même. Einstein s'est moqué un jour de Bohr : "Croyez-vous vraiment que la lune cesse d'exister si vous ne la regardez pas ?". Nous pouvons maintenant lui répondre : En effet. Ou du moins : elle n'existe pas de la manière dont elle existe lorsque nous la regardons. L'homme est co-créateur de la réalité dans laquelle il vit, il ne la subit pas passivement. Mais qu'est-ce qui fait que l'onde en superposition devient une particule ? Est-ce l'acte de mesure ou l'acte d'observation ? La position la plus conservatrice consiste à affirmer que c'est l'appareil de mesure matériel qui modifie ce qui est observé. Dans ce cas, on s'accroche encore - ne serait-ce que d'une main - aux branches des arbres matérialistes. La plupart des physiciens universitaires optent probablement pour cette position. Mais je m'interroge : Einstein ne faisait pas référence à l'acte matériel de mesurer lorsqu'il a mentionné la lune ; il parlait de regarder la lune. Il a clairement interprété la théorie quantique comme une théorie qui considère que c'est l'acte de regarder qui est décisif (même sans équipement de mesure). De même, je m'interroge : nous ne voyons pas le monde qui nous entoure comme une onde en superposition, mais comme un ensemble de particules aux propriétés plus ou moins fixes. Cela n'implique-t-il pas que l'acte de regarder lui-même a provoqué l'effondrement de la fonction d'onde et que la particule est devenue une particule fixe ? Pour paraphraser Einstein : Croyons-nous vraiment que l'effondrement de la fonction d'onde ne se produit pas s'il n'y a pas de physiciens qui mesurent les particules ? Enfin, dans les nombreuses variantes de l'expérience de la double fente, il s'avère qu'une onde devient une particule précisément au moment où la caméra qui l'enregistre effectue un enregistrement sans ambiguïté. Par exemple, si des électrons sont envoyés vers les doubles fentes et que nous enregistrons la position exacte de l'électron avec une caméra utilisant des fréquences lumineuses, on observe qu'au moment précis où la fréquence lumineuse devient suffisamment élevée pour enregistrer l'électron, le modèle d'onde s'effondre et l'électron devient une particule. Ces résultats expérimentaux suggèrent également, à mon avis, que ce qui est décisif n'est pas l'appareil de mesure matériel lui-même - qui reste le même, quelle que soit la fréquence de la lumière - mais plutôt l'acte d'enregistrement ou d'observation lui-même. En d'autres termes, c'est "l'acte de conscience" dans l'observation qui est décisif. Enfin, il se trouve que les fondateurs de la théorie quantique, sur la base de leur théorie et de leurs observations, ont déclaré que la vision matérialiste du monde était incorrecte et se sont orientés vers une vision mystique ou idéaliste du monde, dans laquelle la conscience est considérée comme la cause de la matière (et non l'inverse, comme le prétend le matérialisme). Et si l'on constate que même un personnage aussi admirable que Niels Bohr a quelque peu vacillé sur ce thème - tantôt chaud, tantôt froid -, peut-être faut-il finalement conclure que même les plus grands d'entre nous n'ont pas entièrement surmonté une certaine peur des masses (matérialistes). Mattias |